
1-Guion-Columna-Vertebral.pdf
15 páginas

2-Esqueleto-del-torax.pdf
8 páginas
3-Cavidad-pelvica.pdf
9 páginas

4.-MUSCULOS-DEL-DORSO-Y-NUCA-II.pdf
7 páginas

5-Musculos-del-torax.pdf
6 páginas
6.-MUSCULOS-DEL-ABDOMEN.pdf
4 páginas
7.-Guion-Craneo-21.pdf
7 páginas
8-MUSCULOS-DE-LA-CABEZA-Y-CUELLO.pdf
5 páginas
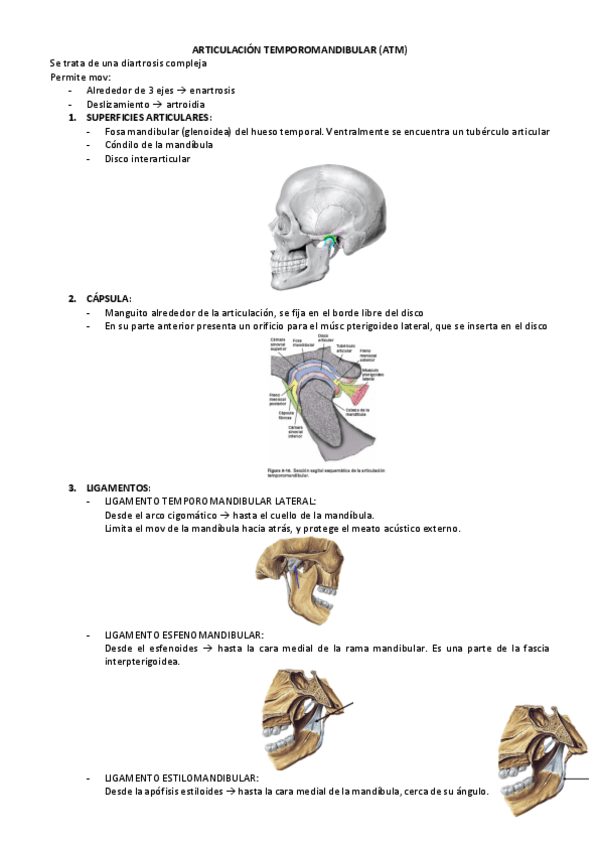
9.-GUION-ATM.pdf
6 páginas

ARTICULACION-COXO-FEMORAL.pdf
10 páginas
MUSCULOS-DE-LA-CADERA.pdf
4 páginas

MUSCULOS-DE-LA-PIERNA.pdf
8 páginas

MUSCULOS-DEL-MUSLO.pdf
6 páginas
MUSCULOS-DEL-PIE.pdf
6 páginas
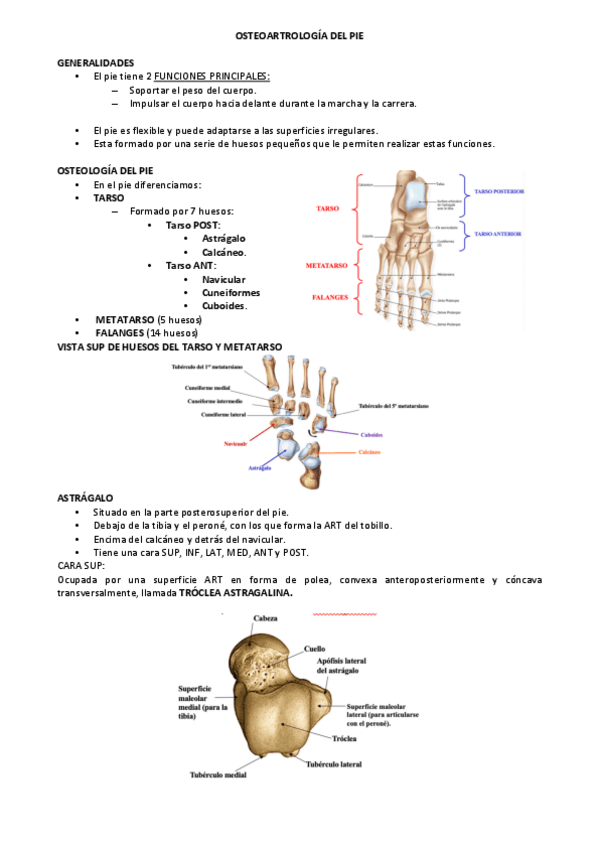
OSTEOARTROLOGIA-DEL-PIE.pdf
9 páginas

RODILLA.pdf
9 páginas
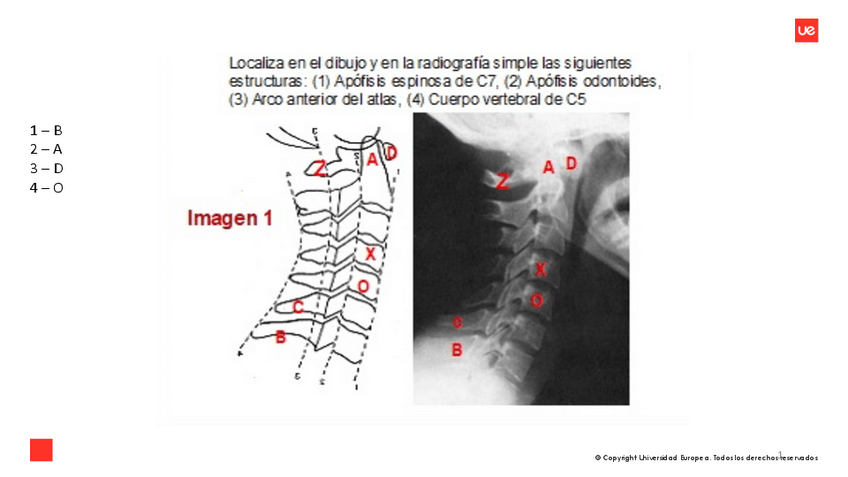
PRACTICAS-TRONCO.pdf
30 páginas
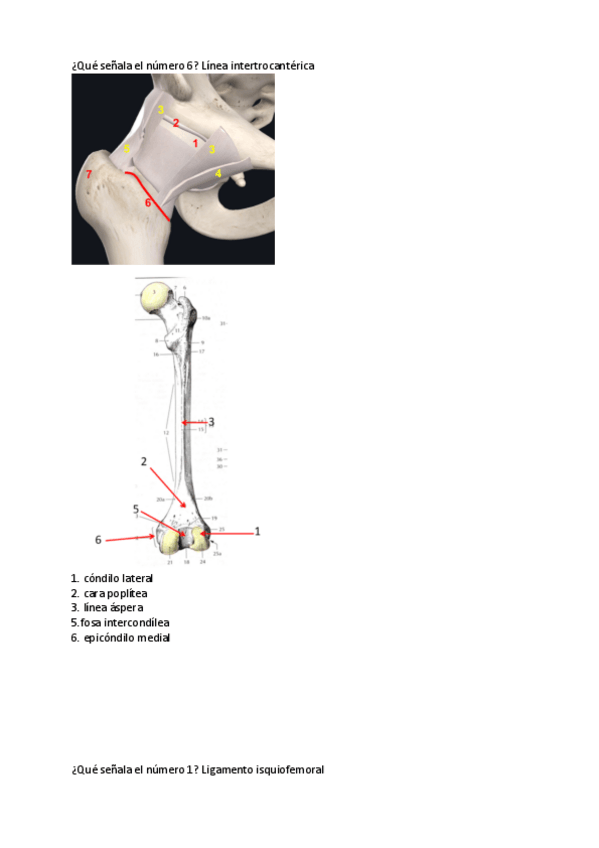
Practicas-MMII--MMSS.pdf
7 páginas

PARCIAL-II-2020.pdf
3 páginas
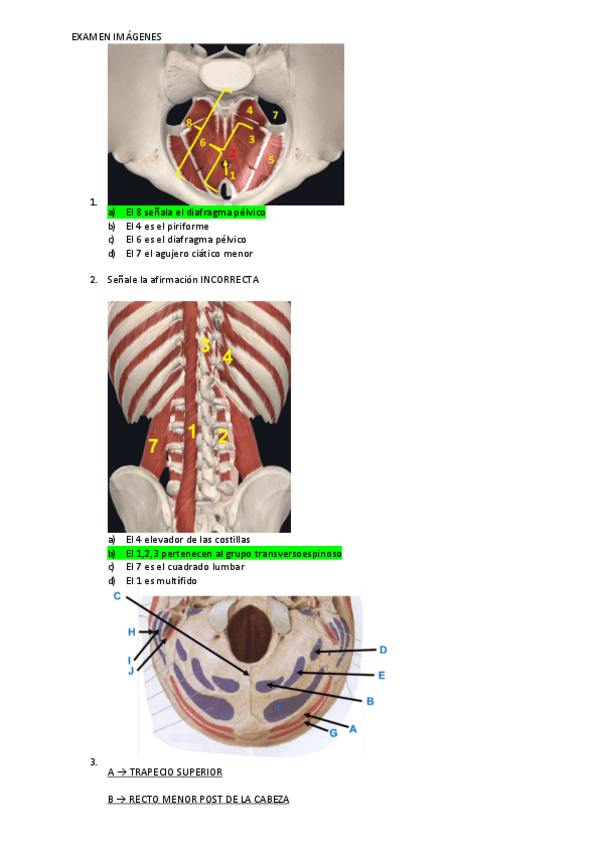
EXAMEN-IMAGENES-2021-22.pdf
7 páginas

PARCIAL-2-ANATOMIA-2021-22.pdf
4 páginas

PARCIAL-1.pdf
3 páginas
content_copy