Tangencia: concepto, tipos y principios

Quédate que en esta entrada te explicamos de manera sencilla qué es la tangencia, los distintos tipos que existen, los principios que la rigen y sus aplicaciones prácticas. ¡Vamos a ello!

¿Qué es la tangencia?

La tangencia es un concepto geométrico que describe el punto en el que una línea toca una curva o superficie sin cortarla.

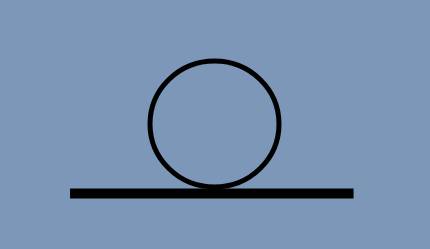
En otras palabras, se llama punto de tangencia al punto en el que dos figuras, por ejemplo una línea y un círculo, se encuentran. Para entenderlo mejor, una tangencia sería cuando una rueda toca el suelo en un solo punto.

Tipos de tangentes

Entender los diferentes tipos de tangencia nos ayuda a visualizar cómo las líneas y las figuras geométricas interactúan en el espacio.

Tangente a un círculo

Una línea es tangente a un círculo si toca el círculo en un solo punto. Matemáticamente, la línea tangente es perpendicular al radio que pasa por el punto de contacto, lo que nos permite calcular fácilmente el ángulo y las distancias implicadas.

Ejemplo: en el caso del borde de una moneda apoyada sobre una mesa, la línea de contacto entre la mesa y el círculo de la moneda es una tangente.

Tangente entre dos círculos

Este tipo de tangencia ocurre cuando dos círculos se tocan en un solo punto, sin superponerse. Existen dos variantes: la tangencia externa y la tangencia interna.

• Tangencia externa: ocurre cuando los dos círculos están fuera uno del otro y solo se tocan en un punto. Un buen ejemplo es el caso de dos burbujas de jabón que se tocan ligeramente por el borde, justo antes de separarse.
• Tangencia interna: sucede cuando un círculo más pequeño está dentro de otro más grande y solo se tocan en un punto del borde. Piensa en una moneda pequeña colocada dentro de una más grande, donde la moneda pequeña toca la grande en un solo punto, formando una tangencia interna.

Este tipo de tangencia es importante en el diseño de engranajes y en la arquitectura de objetos circulares, donde es necesario asegurar que el contacto entre piezas sea preciso y eficiente.

Tangente a una parábola

La tangencia también puede darse entre una línea y una curva más compleja, como una parábola. En este caso, la línea toca la parábola en un solo punto, sin cruzarla. Un ejemplo claro lo encontramos en las antenas parabólicas, donde los rayos de luz o las ondas de radio tocan la superficie parabólica en un punto específico y luego se reflejan hacia un foco, optimizando la recepción de señales.

Ejemplo: imagina un coche subiendo una colina con forma de parábola. Si trazamos una línea tangente en el punto exacto donde el coche toca la pendiente, podemos determinar la inclinación en ese punto, lo que es útil para cálculos de velocidad y aceleración en ingeniería.

Propiedades fundamentales de la tangencia

Las tangencias tienen propiedades que son esenciales para comprender cómo las figuras geométricas interactúan entre sí. Estas propiedades no solo son útiles en problemas matemáticos, sino que también se aplican a situaciones prácticas en ingeniería, diseño y física.

1. Perpendicularidad entre la tangente y el radio
   En el caso de un círculo, la línea tangente en un punto es siempre perpendicular (forma un ángulo de 90 grados) al radio que pasa por ese punto. Si tomamos como ejemplo una bici, el radio de la rueda va desde el centro hasta el punto donde la rueda toca el suelo y la línea que representa el suelo es la tangente.
2. Dos tangentes desde un punto exterior tienen la misma longitud
   Si trazas dos tangentes desde un punto fuera de un círculo, ambas tangentes tendrán la misma longitud. Este principio es fundamental en problemas de geometría y se aplica en construcciones arquitectónicas. Por ejemplo, si tienes un punto externo a una pista circular y quieres construir dos caminos tangentes hacia la pista, ambos caminos tendrán la misma longitud, garantizando simetría.
3. Unicidad de la tangente en un punto
   Desde cada punto de una curva o círculo solo se puede trazar una única tangente. Esto significa que en cualquier punto de una figura geométrica, solo una línea puede tocar la figura sin cortarla. Esta propiedad se aplica en diseño y optimización, como en el caso de lentes ópticas, donde la precisión de la tangente asegura que la luz se refleje correctamente hacia un punto focal.
4. No intersección de la tangente
   Una tangente toca una curva en un solo punto, pero no la corta. Si la línea cortara la figura en dos puntos, ya no sería una tangente, sino una secante. Es decir, en el caso de una pelota deformada o aplastada en el suelo tendría más de un punto de contacto y, por tanto, no se consideraría una tangencia. Esta propiedad es fundamental para evitar puntos de intersección que podrían generar errores en cálculos de distancias o ángulos.

Aplicaciones prácticas de la tangencia

El concepto de tangencia trasciende los libros de matemáticas y al diseño técnico, teniendo numerosas aplicaciones prácticas en distintos campos.

Una de las aplicaciones más comunes de la tangencia está en el diseño de neumáticos. El contacto entre el neumático y la carretera es un punto de tangencia que asegura que el vehículo pueda moverse de manera eficiente y segura. Por lo que conocer este punto de contacto ayuda a optimizar la tracción, el frenado y el control del vehículo.

Por otro lado, en la industria, los engranajes se diseñan utilizando principios de tangencia para que las ruedas dentadas se toquen en un solo punto mientras giran. Este punto de contacto asegura que los engranajes transmitan movimiento de manera eficiente sin deslizarse o perder energía. Así como minimizar la fricción y el desgaste, lo que es clave en máquinas industriales que operan a altas velocidades o que requieren de una precisión extrema.

En la arquitectura, la tangencia es importante para el diseño de puentes y estructuras curvas. Al calcular los puntos de contacto entre los materiales y las fuerzas que actúan sobre ellos, los ingenieros pueden construir estructuras más estables y eficientes. Un ejemplo es el diseño de arcos en puentes, donde las tangentes ayudan a distribuir el peso de manera uniforme y segura, evitando que se concentren fuerzas en un solo punto.

Estas aplicaciones demuestran que la tangencia va más allá de los conceptos teóricos y es una herramienta esencial para resolver problemas prácticos en el diseño y la ingeniería.