El teorema de Tales es una de las bases fundamentales de la semejanza de triángulos. Aunque es un concepto antiguo, su relevancia y aplicabilidad en la vida cotidiana y en diversas áreas de la matemática siguen siendo innegables. A continuación, se presenta un análisis detallado de este teorema.

¿Qué es el teorema de Tales?

El teorema de Tales establece una relación de proporcionalidad entre segmentos de rectas cortadas por líneas paralelas. Nombrado en honor a Tales de Mileto, un matemático y filósofo griego del siglo VI a.C.

Para entenderlo en términos simples, imagine dos rectas que son cortadas por un conjunto de rectas paralelas. Los segmentos que estas paralelas forman en una recta son proporcionales a los segmentos que forman en la otra recta. Es decir, las razones de los segmentos en una recta son iguales a las razones de los segmentos correspondientes en la otra recta.

En el contexto de los triángulos, el teorema de Tales se manifiesta cuando trazamos una línea paralela a uno de los lados de un triángulo, cortando los otros dos lados. Esta línea divide los dos lados en segmentos que son proporcionales entre sí. Como resultado, obtenemos dos triángulos que son semejantes, es decir, tienen la misma forma pero pueden diferir en tamaño.

Fórmula del teorema de Tales

La esencia del teorema de Tales se basa en la proporcionalidad de segmentos cuando dos rectas son cortadas por rectas paralelas. Esta proporcionalidad se puede expresar matemáticamente mediante una fórmula que relaciona los segmentos.

Supongamos que tenemos dos rectas r y s que son cortadas por dos rectas paralelas a y b. Estas paralelas dividen a r en los segmentos A y B y a s en los segmentos A′ y B′.

La fórmula del teorema de Tales establece que:

​

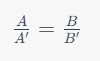
Esto significa que la razón entre los segmentos en la recta r es igual a la razón entre los segmentos en la recta s.

Para visualizarlo mejor, imagine un triángulo ABC con una línea paralela DE al lado AC, cortando AB en D y BC en E. Si aplicamos el teorema de Tales a este escenario, obtenemos:

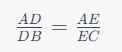
Esto indica que la razón de los segmentos en el lado AB es igual a la razón de los segmentos en el lado BC.

Primer teorema de Tales

Si dos rectas cualesquiera son cortadas por un conjunto de rectas paralelas, entonces los segmentos determinados en una de las rectas son proporcionales a los segmentos correspondientes en la otra recta.

Un ejemplo clásico de la aplicación del primer teorema de Tales es determinar la altura de un objeto inaccesible. Si se tiene un objeto de altura conocida y se mide la sombra que proyecta, y luego se mide la sombra de un objeto de altura desconocida (por ejemplo, un árbol) bajo las mismas condiciones de iluminación, se puede usar la proporcionalidad para determinar la altura del árbol.

Segundo teorema de Tales

Mientras que el primer teorema de Tales se centra en la proporcionalidad de segmentos en rectas cortadas por paralelas, el segundo teorema de Tales se enfoca en la relación entre segmentos dentro de un triángulo cuando una línea corta dos de sus lados de manera paralela al tercer lado.

Dentro de un triángulo, si trazamos una línea que es paralela a uno de sus lados y corta a los otros dos lados, entonces esta línea divide esos dos lados en segmentos que son proporcionales.

Aplicaciones del teorema de Tales

• Medición de distancias inaccesibles: Una de las aplicaciones históricas más famosas del teorema de Tales es la medición de alturas de objetos inaccesibles.
• Cartografía y modelado: En cartografía, se utiliza para mantener proporciones correctas al reducir o ampliar mapas.
• Astronomía: En la antigüedad, el teorema de Tales se utilizaba para calcular distancias entre cuerpos celestes y la Tierra, basándose en observaciones y mediciones angulares.
• Diseño gráfico y arte: Los artistas y diseñadores gráficos utilizan el teorema de Tales para mantener las proporciones correctas al redimensionar imágenes o al crear perspectivas en sus obras.
• Biología y medicina: En estudios de crecimiento y desarrollo, el teorema de Tales puede ayudar a predecir cómo ciertas proporciones en organismos cambian a medida que crecen.

Ejercicios del teorema de tales

1. Ejercicio básico de proporcionalidad: Dado un triángulo ABC, traza una línea DE paralela al lado AC que corta AB en D y BC en E. Si AD = 4 cm, DB = 6 cm, y AE = 5 cm, encuentra la longitud de EC. Solución: 7,5cm.
2. Medición de alturas: Imagina que quieres determinar la altura de un árbol. A las 12 del mediodía, una vara de 2 metros proyecta una sombra de 1 metro. Al mismo tiempo, el árbol proyecta una sombra de 10 metros. ¿Cuál es la altura del árbol? Solución = 20 metros.
3. Aplicación en triángulos: En un triángulo ABC, se traza una línea paralela al lado BC que corta a AB en D y a AC en E. Si AD/DB = 2/3 y AE = 6 cm, encuentra la longitud de EC. Solución = 9 cm.
4. Desafío de proporcionalidad: Dos rectas paralelas cortan las rectas l y m en los puntos A, B y A’, B’ respectivamente. Si AB = 8 cm, A’B’ = 12 cm, y la distancia entre las paralelas en l es de 5 cm, encuentra la distancia entre las paralelas en m. Solución = 7,5cm.

Extensión del teorema de Tales

• Figuras geométricas más complejas: Aunque se aplica comúnmente a triángulos, su principio de proporcionalidad también es válido para otras figuras, como trapecios y paralelogramos, siempre que se mantenga la condición de líneas paralelas.
• Teorema de Tales en el espacio: El teorema puede extenderse a tres dimensiones. Por ejemplo, si un plano paralelo corta dos líneas no coplanares, los segmentos formados en una línea son proporcionales a los segmentos en la otra línea.
• Aplicación en cónicas: En el estudio de las secciones cónicas (elipses, parábolas e hipérbolas), puede utilizarse para probar propiedades y relaciones de semejanza entre diferentes secciones de una cónica.
• Teorema de Tales inverso: Concepto que se deriva del teorema original. Establece que si en dos rectas, los segmentos son proporcionales, entonces las líneas que conectan los puntos correspondientes son paralelas.

Puntos clave

• Es fundamental para la semejanza de triángulos.
• Establece la proporcionalidad de segmentos cuando son cortados por líneas paralelas.
• Tiene aplicaciones prácticas en la vida cotidiana y en la historia de la matemática.
• Se puede extender a otras figuras geométricas más allá de los triángulos.