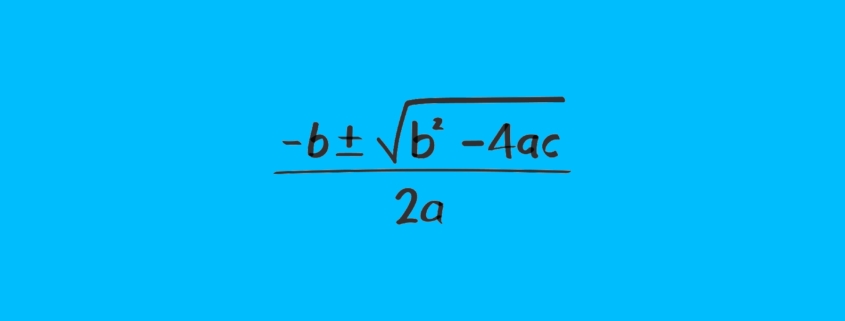Ecuaciones de Segundo Grado: definición, formula y ejemplos

Las ecuaciones de segundo grado, también conocidas como ecuaciones cuadráticas, son una parte fundamental de la matemática y tienen aplicaciones prácticas en diversas áreas como la física, la ingeniería y la economía. Estas ecuaciones se caracterizan por tener una incógnita elevada al cuadrado y son esenciales para entender conceptos más avanzados en matemáticas.

¿Qué es una ecuación de segundo grado?

Una ecuación de segundo grado, o ecuación cuadrática, es una ecuación polinómica donde el grado más alto de la incógnita (generalmente representada por x) es dos.

La forma general de una ecuación de segundo grado es:

ax²+bx+c=0

Donde a, b, y c son constantes, con a≠=0. El término ax² representa el componente cuadrático, bx es el término lineal, y c es el término constante o independiente.

Fórmula ecuación de segundo grado

Para resolver ecuaciones de segundo grado, se utiliza la fórmula cuadrática, que proporciona las soluciones de la ecuación. La fórmula es:

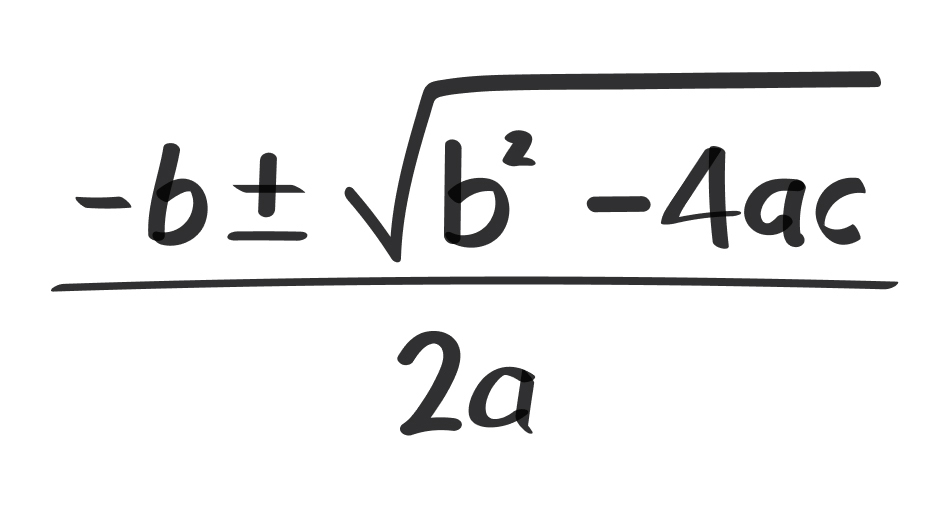
Esta fórmula calcula los valores de x que satisfacen la ecuación original. El término bajo la raíz cuadrada, b²−4ac, es conocido como el discriminante y juega un papel crucial en determinar la naturaleza de las soluciones.

¿Cómo resolver ecuaciones de segundo grado?

Para resolver una ecuación de segundo grado, seguimos estos pasos:

1. Identificar y organizar los términos de la ecuación en la forma ax²+bx+c=0.
2. Calcular el discriminante (b²−4ac).
3. Utilizar la fórmula cuadrática para encontrar los valores de x.

El discriminante determina la naturaleza de las soluciones:

• Si el discriminante es positivo, hay dos soluciones reales y distintas.
• Si es cero, hay una única solución real (las soluciones son iguales).
• Si es negativo, no hay soluciones reales (las soluciones son números complejos).

Ejercicios de ecuaciones cuadráticas

Para practicar, consideremos algunos ejercicios de ecuaciones cuadráticas:

1. Resolver 2x²−3x−5=0.
2. Encontrar las soluciones de x²+4x+4=0.
3. Determinar los valores de x para x²−6x+9=0.

Estos ejercicios ayudan a aplicar la fórmula cuadrática y a entender cómo el discriminante afecta las soluciones.

Soluciones de ecuaciones de segundo grado

Las soluciones de una ecuación de segundo grado pueden ser reales o complejas, dependiendo del discriminante. Cuando las soluciones son reales, pueden ser dos distintas o una doble solución. En el caso de un discriminante negativo, las soluciones son complejas y vienen en pares conjugados.