Asíntota: qué es y su clasificación

Si alguna vez te has preguntado por qué ciertas curvas parecen acercarse infinitamente a una línea sin llegar a tocarla, quédate. En esta entrada te contamos qué es una asíntota, sus tipos y cómo permiten entender el comportamiento de muchas funciones.

¿Qué es una asíntota?

Una asíntota es una línea recta que actúa como «límite» para una función matemática. Aunque la curva de la función se acerque infinitamente a esta línea, nunca la toca ni la cruza, al menos en un tramo específico de su dominio.

Estas líneas nos ayudan a analizar el comportamiento de las funciones cuando las variables se acercan a ciertos valores extremos, como el infinito o a valores críticos del dominio.

Existen tres tipos de asíntotas: horizontales, verticales y oblicuas. Cada una describe un aspecto diferente del comportamiento de la curva y se utilizan dependiendo de la forma de la función que estamos estudiando.

Por ejemplo, en la función de abajo, la curva se acerca infinitamente a los ejes x e y, sin llegar nunca a tocarlos. Estos ejes son asíntotas y analizarlos nos permite comprender cómo «se mueven» los valores de la función.

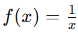
Asíntotas horizontales

Las asíntotas horizontales son líneas rectas paralelas al eje x que indican el valor al que la función se aproxima cuando la variable independiente (x) tiende a infinito positivo o negativo. Matemáticamente, estas asíntotas se determinan evaluando el límite de la función cuando x→∞ o x→−∞.

Por ejemplo, en la función:

Al calcular el límite cuando x→∞, obtenemos lim⁡_x→∞ f(x)=0. Esto significa que la línea y=0 es una asíntota horizontal. Aquí la curva se acerca cada vez más a esta línea conforme x aumenta o disminuye en valor absoluto.

Un detalle importante es que una función puede tener una o ninguna asíntota horizontal, pero nunca más de una por cada dirección del infinito. Las asíntotas horizontales son útiles para entender cómo se comportan las funciones a largo plazo, especialmente en análisis de datos, economía, física o biología.

Asíntotas verticales

Una asíntota vertical es una línea recta paralela al eje y que tiende a infinito positivo o negativo. Estas líneas se encuentran en los valores del dominio donde la función no está definida, como los denominadores que se hacen cero en una fracción.

Por ejemplo, en la función:

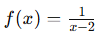
La curva tiene una asíntota vertical en x=2, porque en este punto el denominador se convierte en cero, lo que hace que la función no esté definida. Al acercarse a x=2 desde ambos lados, los valores de f(x) crecen sin límite, indicando una asíntota en esa posición.

Es importante recordar que las asíntotas verticales no representan valores que la función alcanza, más bien, marcan límites donde la función no puede existir. Esto es común en funciones racionales, logarítmicas y trigonométricas con restricciones.

Asíntotas oblicuas

Las asíntotas oblicuas son un tipo especial que aparece cuando la función no se acerca ni a una línea horizontal ni a una vertical, sino a una línea diagonal en forma de recta inclinada. Estas suelen aparecer en funciones racionales donde el grado del numerador es mayor al del denominador por exactamente una unidad.

Por ejemplo, en la función:

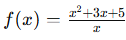
Al dividir los términos, obtenemos:

​

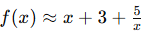
En este caso, y=x+3 es una asíntota oblicua, porque conforme x→∞ o x→−∞, la curva se acerca a esta línea inclinada.

Para calcular estas asíntotas, usamos la división polinómica para descomponer la función en una recta más un residuo que tiende a cero en el infinito. Estas líneas son menos comunes, pero son fundamentales en el análisis de funciones de física teórica o ingeniería.

¿Cómo identificar las asíntotas en una función?

Aquí un esquema sencillo:

1. Horizontales: calcula lim⁡x→∞ y lim⁡x→−∞. Si ambos límites existen y son finitos, estas son las asíntotas horizontales.
2. Verticales: busca los valores donde el denominador de la función sea cero o la función no esté definida. Evalúa el límite en estos puntos para verificar si tiende a infinito.
3. Oblicuas: si el grado del numerador supera al denominador por una unidad, divide los polinomios para encontrar la ecuación de la asíntota.