Binomio de Newton: Teorema, formula y explicación
¿Que es el Binomio de Newton? ¿Cual es su formula? ¿Cómo se calcula?
Si estas estudiando Algebra el binomio de Newtom es un tema fundamental que debes conocer. Es una fórmula que permite expandir la potencia de un binomio. Aunque puede parecer un concepto abstracto, tiene aplicaciones prácticas en diversos campos, desde la física hasta la economía. En este artículo, exploraremos la historia, la fórmula, las propiedades y las aplicaciones prácticas del binomio de Newtom.
Tabla de contenidos
¿Qué es el Binomio de Newton?
El Binomio de Newton, tambien nombrado como teorema del binomio, es especialmente útil cuando se trata de expandir binomios elevados a potencias más altas, donde la multiplicación manual sería tediosa. Por ejemplo, expandir (a+b)5 manualmente requeriría múltiples multiplicaciones, mientras que con el Binomio de Newton, se puede hacer de manera más sistemática y rápida.
El Binomio de Newton es una fórmula que facilita el cálculo de la potencia de un binomio. Específicamente, se utiliza para descomponer y resolver expresiones algebraicas de la forma (a+b)n, donde ‘a‘ y ‘b‘ son términos y ‘n‘ es un exponente entero positivo.
Potencias de un binomio
Las potencias de un binomio se refieren a la elevación de un binomio a un exponente entero positivo. Es decir, si tenemos un binomio de la forma (a+b), podemos elevarlo a cualquier potencia n, donde n es un número entero positivo. La expansión de estas potencias se basa en el binomio de Newton.
¿Cómo se calcula la expansión de un binomio?
La expansión de un binomio es un proceso que permite descomponer un binomio elevado a una potencia en una serie de términos. Esta expansión se basa en el teorema o Binomio d e Newton.
Los numeros combinatorio, tambien conocidos como coeficiente binomial, son una parte crucial de la expansión. Estos coeficientes indican cuántas formas se pueden seleccionar k elementos de un conjunto de n elementos sin tener en cuenta el orden.

Fórmula del binomio de Newton
La fórmula del binomio de Newton es esencial para expandir potencias de binomios. Aunque puede parecer compleja al principio, con la práctica se vuelve más intuitiva.
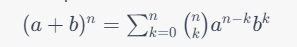
Donde:
es el coeficiente binomial, tambien conocido como número combinatorio y es igual a
- an – k y bk son las potencias de los términos ‘a’ y ‘b’ respectivamente
- La suma se extiende desde k=0 hasta k=n
Propiedades del binomio de Newton
El binomio de Newton tiene varias propiedades clave:
- Al expandir el binomio de Newton, siempre se obtiene un término más que el grado del binomio.
- Las potencias del primer elemento comienzan con el grado del binomio y disminuyen hasta 0.
- Las potencias del segundo elemento comienzan en 0 y aumentan hasta el grado del binomio.
- Para cada término, la suma de los exponentes es igual al grado del binomio.
Binomio de Newton negativo: potencia de una resta
Cuando hablamos de un binomio de Newton negativo, nos referimos a la expansión de un binomio que tiene una resta, es decir, una expresión de la forma (a−b)n. Esta forma particular introduce una serie de características y patrones únicos en la expansión.
- Al expandir un binomio que contiene una resta, los signos de los términos resultantes alternarán. Esto se debe a las propiedades de las potencias de números negativos.
- Al aplicar la fórmula del Binomio de Newton a (a−b)n, se observa que los coeficientes binomiales siguen siendo los mismos que en la expansión de (a+b)n. Sin embargo, debido al término negativo, los signos de los términos resultantes alternarán.
- Si n es impar, el signo del término con b a la primera potencia será negativo.
- Si n es par, todos los términos resultantes serán positivos.
Binomio de Newton: ejercicios
Practicar con ejercicios es esencial para consolidar la comprensión y aplicación del Binomio de Newton. A través de estos ejercicios, uno puede familiarizarse con la fórmula, el uso de coeficientes binomiales y la expansión de binomios a diversas potencias. A continuación, se presentan algunos ejercicios representativos, junto con soluciones y consejos:
Ejercicio básico:
Expanda el binomio (x+y)2.
Solución:
Utilizando la fórmula del Binomio de Newton, obtenemos:
(x+y)2=x2+2xy+y2.
Ejercicio con coeficientes:
Expanda el binomio (2x−3y)3.
Solución:
Aplicando la fórmula del Binomio de Newton:
(2x−3y)3=(2x)3−3(2x)2(3y)+3(2x)(3y)2−(3y)3
Simplificando, obtenemos:
8x3−36x2y+54xy2−27y3.
Ejercicio con potencia más alta:
Expanda el binomio (a+b)4.
Solución:
Usando el Triángulo de Pascal o la fórmula del Binomio de Newton:
(a+b)4=a4+4a3b+6a2b2+4ab2+b4.
Historia del binomio de Newton
Aunque el nombre «binomio de Newton» rinde homenaje al célebre científico inglés Isaac Newton (1642-1727), la primera formulación del teorema fue descubierta por el ingeniero persa Al-Karijí alrededor del año 1000. Además, durante el siglo XIII, los matemáticos chinos Yang Hui y Chuh Shih-Chieh ya estaban familiarizados con las expansiones binomiales de grados bajos.
En el siglo XVII, Newton construyó sobre las bases establecidas por matemáticos anteriores y expandió el teorema del binomio. Utilizó métodos de interpolación y extrapolación, junto con conceptos de exponentes generalizados, para transformar una expresión polinómica en una serie infinita. Newton también demostró que el exponente n del teorema del binomio podía ser racional o incluso negativo, llevando a series infinitas en ambos casos.
Binomio de Newton – Puntos clave
- El binomio de Newton es una herramienta para expandir potencias de binomios.
- Los coeficientes binomiales en la expansión provienen de números combinatorios.
- El triángulo de Pascal es una herramienta útil para encontrar coeficientes binomiales rápidamente.
¿Qué relación hay entre el triángulo de Pascal, el binomio de Newton y los productos notables?
El triángulo de Pascal, también conocido como triángulo de Tartaglia, es una representación matemática de números ordenados en forma de triángulo. Cada número en el triángulo de Pascal representa un coeficiente binomial. Estos coeficientes son esenciales para la expansión del binomio de Newton. Por lo tanto, el triángulo de Pascal proporciona una forma rápida y conveniente de encontrar coeficientes binomiales para la expansión de binomios, facilitando el proceso de expansión y simplificación de productos notables.


