Campana de Gauss: Concepto, fórmula y representación

La campana de Gauss, o distribución normal, se caracteriza por su uso estadístico y matemático. Tiene una capacidad para describir y modelar fenómenos naturales y sociales.

En este artículo vamos a profundizar en su concepto, propiedades y aplicaciones en diferentes campos.

¿Qué es la campana de Gauss?

La campana de Gauss es una representación gráfica de la distribución normal de un conjunto de datos. La forma de la distribución es simétrica y recuerda a una campana, de ahí su nombre.

Históricamente, aunque Gauss es a menudo asociado con esta distribución, fue Abraham de Moivre quien primero la describió en el contexto de aproximaciones binomiales, y Laplace quien la expandió en su trabajo sobre la teoría analítica de las probabilidades.

Fórmula de la campana de Gauss

La campana de Gauss se caracteriza por su forma simétrica alrededor de un valor central, que es la media de la distribución. Matemáticamente, se describe mediante la siguiente ecuación:

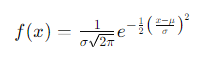
Donde:

• μ es la media o el promedio de los datos.
• σ es la desviación estándar, que mide cuánto se dispersan los datos alrededor de la media.
• e es la base del logaritmo natural.
• x representa los valores de los datos.

Representacioón de la campana de Gauss

La curva tiene su punto más alto en la media, y su altura disminuye simétricamente a medida que nos alejamos de este punto central. La desviación estándar determina el ancho de la campana: una desviación estándar grande significa una curva más ancha y plana, indicando una mayor dispersión de los datos.

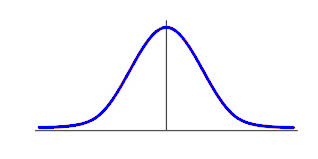
Características de la campana de Gauss o distribución normal

La distribución normal, representada por la campana de Gauss, posee características distintivas.

• Simetría y Forma de Campana: Esto significa que los datos se distribuyen de manera uniforme a ambos lados del valor medio. La forma de la curva es acampanada, con la mayoría de los datos concentrados cerca del centro y menos datos a medida que nos alejamos hacia cualquiera de los dos extremos.
• Media, Mediana y Moda: En una distribución normal perfecta, la media, la mediana y la moda son iguales y se encuentran en el punto más alto de la campana.
• Desviación Estándar y Varianza: En la distribución normal, aproximadamente el 68% de los datos se encuentran dentro de una desviación estándar de la media, el 95% dentro de dos desviaciones estándar, y el 99.7% dentro de tres desviaciones estándar. Esta regla es conocida como la regla empírica o la regla 68-95-99,7.

Significado e interpretación del valor esperado y la desviación estándar en la campana de Gauss

La campana de Gauss no solo es fundamental por su forma y simetría, sino también por los conceptos estadísticos clave que incorpora: el valor esperado (o media) y la desviación estándar.

El valor esperado, comúnmente conocido como la media (μ), es una medida de tendencia central en la distribución normal. En una distribución normal, la media es el punto en el que la curva alcanza su máximo y es el centro de simetría de la distribución.

La desviación estándar (σ) proporciona una medida de cuánto se dispersan los valores de los datos alrededor de la media.

El valor esperado (media) y la desviación estándar son fundamentales para interpretar la distribución normal.

¿Qué tipos de fenómenos o datos se pueden modelar con una campana de Gauss?

La campana de gauss se puede aplicar a muchos campos. Esta sección explora varios ejemplos de fenómenos y tipos de datos que típicamente siguen una distribución normal.

Ejemplos en Ciencias Naturales y Sociales

1. Mediciones Biológicas: Muchas características biológicas, como la altura, el peso y la presión arterial en humanos, tienden a modelarse con la campana de gauss en una población.
2. Resultados de Pruebas Académicas: Las puntuaciones en exámenes estandarizados, como el SAT o GRE, a menudo siguen una distribución normal, con la mayoría de los estudiantes obteniendo puntuaciones cerca del promedio y menos estudiantes obteniendo puntuaciones muy altas o muy bajas.
3. Fenómenos Psicológicos: Características como el coeficiente intelectual (CI) y ciertos rasgos de personalidad tienden a distribuirse de manera normal en la población general.
4. Errores de Medición: En experimentos científicos y encuestas, los errores de medición suelen distribuirse normalmente alrededor de un valor central de cero.

Ejemplos Aplicaciones en Tecnología y Negocios

1. Control de Calidad: En la fabricación y producción industrial, las variaciones en las dimensiones de los productos suelen seguir la campana de gauss, lo que permite a los ingenieros de calidad aplicar técnicas estadísticas para el control de calidad.
2. Finanzas y Economía: Los rendimientos de los activos financieros, como las acciones y los bonos, a menudo se modelan utilizando una distribución normal, aunque esta aproximación puede tener limitaciones, especialmente en situaciones de mercado extremas.

Importancia de la campana de Gauss en el análisis de datos

La campana de Gauss o distribución normal tiene una amplia aplicación en el análisis de datos y la toma de decisiones crucial debido a su capacidad para modelar y predecir comportamientos y tendencias.

• En estadística inferencial, la campana de gauss o distribucción normal es la base de muchas pruebas estadísticas, como la prueba t de Student y la prueba de chi-cuadrado, que permiten hacer inferencias sobre poblaciones más grandes a partir de muestras de datos. Además, los intervalos de confianza para estimaciones de la media se construyen a menudo bajo la suposición de normalidad, proporcionando una forma de expresar la incertidumbre en las estimaciones de los parámetros.

• En la investigación científica, la distribución normal ayuda a entender y analizar datos que se agrupan alrededor de un valor central, siendo útil en estudios que involucran mediciones biológicas, comportamientos humanos y fenómenos naturales.

• En el ámbito empresarial, la comprensión de la distribución normal permite interpretar tendencias y patrones de consumo, así como predecir comportamientos futuros de los clientes en el análisis de mercado. Además, en finanzas y seguros, se utiliza para modelar riesgos y calcular probabilidades, lo que es fundamental para la toma de decisiones estratégicas y la gestión financiera.

En educación, especialmente en la evaluación y calificación de los estudiantes, la distribución normal facilita la comprensión del rendimiento estudiantil y el establecimiento de criterios de evaluación justos y equitativos.