Distancia entre Dos Puntos: Formula y cómo se calcula
La distancia entre dos puntos es importante en matemáticas, física y otras disciplinas. Permite medir el espacio entre dos ubicaciones en un plano o espacio. Es crucial para resolver problemas geométricos, pero también es útil en la vida diaria, como en la navegación GPS o el diseño arquitectónico.
En este artículo, exploraremos cómo se calcula la distancia entre dos puntos, comenzando por la fórmula básica utilizada en un plano bidimensional, extendiéndonos hacia su relación con el teorema de Pitágoras, y luego avanzando hacia conceptos más complejos como la distancia euclidiana y la distancia de Manhattan.
Tabla de contenidos
¿Cómo se calcula la distancia entre dos puntos?
En un plano bidimensional, un punto se define por un par de coordenadas: (x, y), donde «x» representa la posición en el eje horizontal y «y» la posición en el eje vertical. Estas coordenadas nos permiten ubicar de manera precisa cualquier punto en dicho plano.
Imaginemos que tenemos dos puntos, P1 y P2, con coordenadas (x1, y1) y (x2, y2), respectivamente.
La distancia entre estos dos puntos puede ser visualizada como la longitud de la línea recta que los une.
Para calcular esta longitud, podemos utilizar un enfoque geométrico basado en el teorema de Pitágoras, el cual establece que en un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de los cuadrados de las longitudes de los otros dos lados.
Podemos imaginar un triángulo rectángulo formado por los puntos P1 y P2, donde la distancia que queremos calcular es la hipotenusa, y los otros dos lados del triángulo son las diferencias entre las coordenadas x e y de los puntos P1 y P2. Así, el lado horizontal del triángulo tiene una longitud de |x2 – x1|, y el lado vertical tiene una longitud de |y2 – y1|. Utilizando el teorema de Pitágoras, podemos encontrar la longitud de la hipotenusa, que es la distancia directa entre los dos puntos
Fórmula para calcular la distancia entre dos puntos
La fórmula para calcular la distancia entre dos puntos en un plano bidimensional se deriva directamente del teorema de Pitágoras, que hemos discutido anteriormente. La fórmula se expresa como:
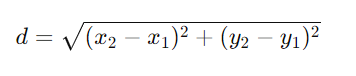
Donde:
- d es la distancia entre los dos puntos,
- (x1, y1) son las coordenadas del primer punto,
- (x2, y2) son las coordenadas del segundo punto.
¿Cuál es la relación entre la distancia entre dos puntos y el teorema de Pitágoras?
Según el teorema de Pitágoras en cualquier triángulo rectángulo, el cuadrado de la longitud de la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de los cuadrados de las longitudes de los otros dos lados, conocidos como catetos.
La relación entre este teorema y la distancia entre dos puntos se hace evidente cuando consideramos cómo medimos la distancia en un plano bidimensional (o en un espacio tridimensional, extendiendo los principios). Al tratar de calcular la distancia directa entre dos puntos, efectivamente estamos buscando la longitud de la hipotenusa de un triángulo rectángulo imaginario, cuyos catetos están definidos por las diferencias en las coordenadas x y y de estos puntos.
La distancia euclidiana: para calcular la distancia entre dos puntos
La distancia euclidiana es quizás la forma más conocida y utilizada para calcular la distancia entre dos puntos, ya sea en un plano bidimensional o en espacios de mayor dimensionalidad.
En un plano bidimensional se calcula usando la fórmula que hemos discutido anteriormente:
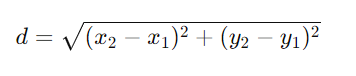
Esta fórmula se puede extender a tres dimensiones para calcular la distancia entre dos puntos en el espacio tridimensional, incorporando una tercera coordenada, z. En este caso, si tenemos dos puntos P1(x1, y1, z1) y P2(x2, y2, z2), la fórmula se amplía a:
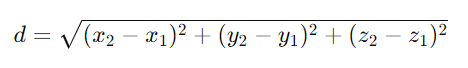
Esta extensión a tres dimensiones sigue el mismo principio que en dos dimensiones: calcular la hipotenusa de un triángulo en tres dimensiones formado por las diferencias en cada una de las coordenadas de los puntos.
En un espacio de n dimensiones, la distancia euclidiana entre dos puntos P1(x11, x12, …, x1n) y P2(x21, x22, …, x2n) se generaliza como:
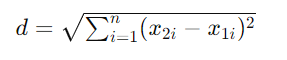
Medir la distancia entre 2 puntos con la distancia de Manhattan
La distancia de Manhattan mide la distancia entre dos puntos moviéndose solo a lo largo de ejes ortogonales. Esto es, se puede mover horizontal o verticalmente, pero no en diagonal. Este nombre proviene de las cuadrículas urbanas como las de Manhattan, donde las calles y avenidas crean un patrón de cuadrícula que limita el movimiento a lo largo de las líneas de la cuadrícula.
La fórmula para calcular la distancia de Manhattan entre dos puntos P1(x1, y1) y P2(x2, y2) en un plano bidimensional es la siguiente:
dManhattan= ∣x2 − x1∣ +∣y2 − y1∣
Donde:
- ∣x2 − x1∣ es el valor absoluto de la diferencia entre las coordenadas x de los dos puntos, que representa la distancia horizontal.
- ∣y2 − y1∣ es el valor absoluto de la diferencia entre las coordenadas y de los dos puntos, que representa la distancia vertical.
Ejercicios sobre distancia entre dos puntos
Ejercicio 1: Distancia Euclidiana en el Plano
Dados los puntos A(2, 3) y B(5, 7), calcula la distancia euclidiana entre ellos.
Solución: Utiliza la fórmula de la distancia euclidiana en dos dimensiones.
Ejercicio 2: Distancia de Manhattan en el Plano
Considera los mismos puntosA(2, 3) y B(5, 7). Calcula la distancia de Manhattan entre ellos.
Solución: Aplica la fórmula de la distancia de Manhattan.
Ejercicio 3: Distancia Euclidiana en el Espacio
Dados los puntos C(1, 2, 3) y D(4, 6, 8), calcula la distancia euclidiana entre ellos en un espacio tridimensional.
Solución: Extiende la fórmula de la distancia euclidiana para tres dimensiones.


