Integral definida: concepto, propiedades y cálculo

La integral definida tiene múltiples aplicaciones en las distintas ramas de la ciencia. Sigue leyendo este artículo que te contamos qué es, sus propiedades y cómo calcularlas con un ejemplo práctico.

¿Qué es una integral definida?

La integral definida se utiliza para encontrar el área bajo una curva en un intervalo cerrado [a,b]en el eje x.

Matemáticamente, la integral definida de una función f(x) en el intervalo [a,b] se representa como:

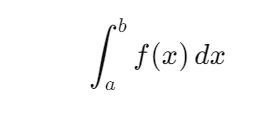
En esta expresión:

• a y b son los límites de integración que definen el intervalo sobre el cual se está calculando el área.
• f(x) es la función que se va a integrar.
• dx indica que la integración se realiza respecto a la variable x.

Si la curva está por encima del eje x, el área es positiva y si está por debajo, el área es negativa. Además la integral definida es capaz de combinar estas áreas, permitiendo calcular tanto el área total como la acumulación neta de valores de la función en ese intervalo.

Propiedades de la integral definida

La integral definida tiene varias propiedades importantes que facilitan su cálculo y comprensión, te las mostramos a continuación:

• Linealidad: La integral definida es lineal, lo que significa que si f(x) y g(x) son funciones integrables y c es una constante, entonces:

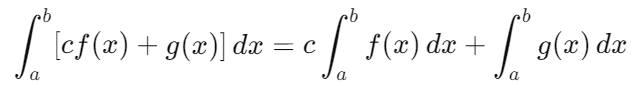
• Propiedad aditiva: Si se divide el intervalo de integración en dos subintervalos [a,c] y [c,b], la integral sobre el intervalo total [a,b] es la suma de las integrales sobre los subintervalos:

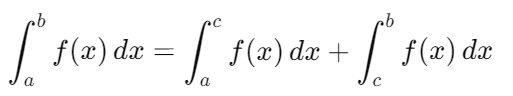
• Cambio de límites: Si se invierten los límites de integración, el signo de la integral cambia:

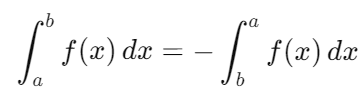
• Integral de una constante: La integral de una constante c sobre un intervalo [a,b] es igual a la constante multiplicada por la longitud del intervalo:

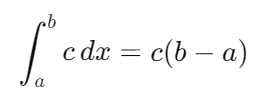
• Valor medio del teorema del cálculo: Existe un punto c en el intervalo [a,b] tal que:

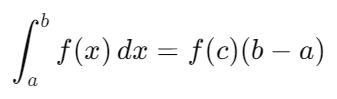
Esto significa que el área bajo la curva es igual al valor de la función en algún punto del intervalo, multiplicado por la longitud del intervalo.

Tabla de integrales definidas

Para facilitar el cálculo de integrales definidas, se utilizan tablas que contienen integrales comunes:

Cálculo de una integral definida

Para calcular una integral definida se deben seguir los siguientes pasos:

1. Encontrar la antiderivada: es decir, hallar la función primitiva o antiderivada F(x) de la función f(x) o lo que es lo mismo encontrar una función cuya derivada sea f(x).

2. Aplicar la regla fundamental del cálculo: Una vez que obtenida la antiderivada F(x), se aplica la regla fundamental del cálculo que establece que:

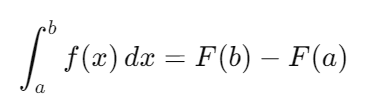
Es decir, se evalúa la antiderivada en los límites superior e inferior y se resta el valor de F(a)F(a)F(a) del valor de F(b)F(b)F(b).

3. Simplificar el resultado: Finalmente, se realiza la simplificación necesaria para obtener el valor de la integral definida.

Ejemplo de cálculo:

Calculemos la integral definida de la función f(x)=3x² en el intervalo [1,4]:

Lo primero será encontrar la antiderivada de 3x² que es F(x)=x³, ya que la derivada de x³ es 3x².

Si aplicamos ahora la regla fundamental del cálculo:

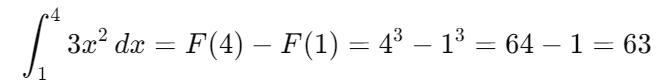
Concluiremos que el resultado de la integral definida es 63, que representa el área bajo la curva 3x² desde x=1 hasta x=4.