Métodos de integración: concepto y ejemplos
Aunque algunas integrales pueden resolverse de manera directa, otras, al ser más complejas, requieren de unos métodos o técnicas especiales para llegar a una solución. En esta entrada te contamos cada uno de estos métodos de integración para que entiendas cuándo y cómo usarlos, con ejemplos prácticos para facilitar su comprensión.
Tabla de contenidos
¿Qué son los métodos de integración?
Los métodos de integración son técnicas matemáticas que nos ayudan a resolver integrales que no pueden resolverse de manera directa.
Cuando una integral es demasiado compleja para resolverse con métodos básicos, estos procedimientos avanzados nos permiten descomponerla en partes más sencillas de resolver. Cada método se basa en un conjunto específico de reglas y es adecuado para ciertos tipos de funciones, facilitando el cálculo de integrales que de otro modo serían inabordables.
A continuación pasamos a desarrollar los 5 métodos de integración más importantes:
- Integración por cambio de variable.
- Integración por partes.
- Integración de funciones trigonométricas.
- Integración de funciones racionales
- Integración de funciones exponenciales
Método de integración: Integración por cambio de variable
La integración por cambio de variable es uno de los métodos más utilizados y se basa en transformar una función complicada en otra más sencilla. Este método es útil cuando se tiene una expresión compuesta de una función y su derivada, porque permite simplificar la expresión al cambiar la variable.
Fórmula básica:
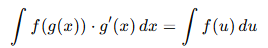
Donde u= g(x) y du= g'(x) dx. Es decir, se cambia la variable x por una nueva variable u para simplificar la integral.

Método de integración: Integración de funciones trigonométricas
La integración de funciones trigonométricas aprovecha las identidades trigonométricas para simplificar la función antes de integrarla. Este método es especialmente útil cuando se encuentran potencias de senos, cosenos o productos de estas funciones.

Método de integración: Integración de funciones racionales
Este método se aplica a funciones racionales, que son aquellas que pueden expresarse como el cociente de dos polinomios. El método común para este tipo de funciones es la descomposición en fracciones parciales, que convierte una fracción complicada en una suma de fracciones más simples, facilitando la integración.

Método de integración: Integración por partes
La integración por partes es una herramienta poderosa para integrar productos de funciones y se basa en la fórmula:

En esta fórmula, elegimos una función u para derivar y otra dv para integrar. Este método es útil cuando la derivada de una función es más simple que la función original.

Método de integración: Integración de funciones exponenciales con variables en el exponente
Las funciones exponenciales donde la variable está en el exponente son comunes, y para estas integrales, el uso de factores de ajuste suele ser necesario. Este tipo de integración es común en cálculos de crecimiento, interés compuesto y fenómenos de desintegración.

Este ajuste facilita el proceso cuando las funciones exponenciales tienen coeficientes distintos de 1 en el exponente.


