Multiplicación de matrices: qué es, propiedades y ejemplos
Multiplicar matrices es más sencillo de lo que parece a prioiri. En esta entrada, te guiamos paso a paso para que aprendas a multiplicarlas, conozcas sus propiedades y descubras las distintas aplicaciones prácticas que tiene en economía, física e informática.
Tabla de contenidos
¿Qué es la multiplicación de matrices?
La multiplicación de matrices es un proceso matemático que permite combinar dos matrices para obtener una tercera matriz, llamada producto.
La multiplicación de matrices requiere que las matrices involucradas tengan dimensiones compatibles. Es decir, para multiplicar una matriz de 2×3 (dos filas, tres columnas) por otra matriz, esta segunda matriz debe tener 3 filas.
Propiedades de la multiplicación de matrices
Para entender mejor la multiplicación de matrices, es importante conocer sus propiedades principales. Estas propiedades, además de definir cómo funciona la operación, ofrecen atajos para resolver problemas más complejos.
Propiedad no conmutativa
En la multiplicación de matrices el orden de los factores sí afecta al producto:
A×B no es igual a B×A
Si tenemos dos matrices A y B, al calcular A×B obtendremos un resultado diferente al de B×A. Incluso, en algunas situaciones, puede que no podamos realizar la operación ya que la multiplicación de matrices requiere que el número de columnas de la primera matriz sea igual al número de filas de la segunda.
Propiedad asociativa
Aunque la multiplicación de matrices no es conmutativa, sí es asociativa. Esto quiere decir que si tenemos tres matrices A, B y C, el producto:
(A×B)×C es igual a A×(B×C)
Esta propiedad permite agrupar matrices para simplificar cálculos complejos sin alterar el resultado. Por ejemplo, si tenemos que multiplicar varias matrices en una larga operación, esta propiedad da flexibilidad para hacer los cálculos en el orden que te resulte más conveniente.
Propiedad distributiva respecto a la suma
La multiplicación de matrices es distributiva respecto a la suma. Esto quiere decir que, si tenemos una matriz A y queremos multiplicarla por la suma de dos matrices B y C, el resultado es el mismo que si multiplicamos A por B y A por C por separado y luego sumamos los resultados:
A×(B+C)= A×B + A×C
Esto es útil cuando queremos descomponer una matriz en varias partes para simplificar el proceso de cálculo.
¿Cómo se multiplican las matrices?
Multiplicar matrices es muy sencillo, tan solo tienes que seguir los pasos que vamos a ver en el siguiente ejemplo:
Supongamos que tenemos dos matrices, A y B:
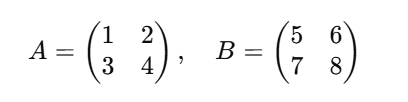
Para calcular A×B, multiplicamos cada elemento de la fila de A por cada elemento de la columna correspondiente de B y luego sumamos estos productos:
- El elemento en la posición (1,1) es 1×5+2×7=5+14=19
- El elemento en la posición (1,2) es 1×6+2×8=6+16=22
- El elemento en la posición (2,1) es 3×5+4×7=15+28=43
- El elemento en la posición (2,2) es 3×6+4×8=18+32=50
El producto de A×B es, por tanto:
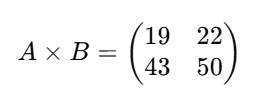
Aplicaciones prácticas de la multiplicación de matrices
La multiplicación de matrices tiene una amplia variedad de aplicaciones. A continuación, destacamos las más importantes:
Una de las aplicaciones más comunes es en el campo de la informática y la programación de gráficos. En este ámbito, la multiplicación de matrices se usa para manipular gráficos en 3D, como rotaciones, traslaciones y escalas. Gracias a esta operación, los videojuegos y las simulaciones pueden mover personajes y objetos en entornos complejos.
Por otro lado, en economía y finanzas, las matrices ayudan a analizar grandes volúmenes de datos. Por ejemplo, en modelos de análisis de riesgo, se utilizan matrices para representar escenarios financieros y calcular resultados en función de variables específicas.
En la física, la multiplicación de matrices es fundamental para resolver sistemas de ecuaciones que modelan fenómenos naturales, como la transmisión de fuerzas o el flujo de energía en un sistema cerrado. Los físicos utilizan matrices para simplificar estos problemas, haciendo posible predecir comportamientos complejos en un sistema de una manera más sencilla.


