Producto escalar: qué es, propiedades y cálculo

El producto escalar es uno de los conceptos que debes dominar a la hora de trabajar con vectores en matemáticas y en física. A lo largo de esta entrada, profundizaremos en qué consiste, sus propiedades y sus distintas aplicaciones de la mano de ejemplos para mejorar su comprensión.

¿Qué es el producto escalar?

Es una operación matemática que se realiza entre dos vectores y da como resultado un número real.

Este valor numérico nos ayuda a entender cuánta influencia tiene un vector sobre otro. Si el producto escalar entre dos vectores es cero, significa que son perpendiculares entre sí. En cambio, si el resultado es positivo, los vectores apuntan en la misma dirección (o en direcciones similares) y si el resultado es negativo, los vectores apuntan en direcciones opuestas.

Propiedades del producto escalar

Estas propiedades simplifican el cálculo de vectores y ofrecen una mejor comprensión de cómo interactúan los vectores ante diferentes situaciones:

Propiedad Conmutativa

El orden de los vectores no afecta al resultado. Es decir, no importa el orden en el que multipliques los vectores, que siempre obtendrás el mismo resultado.

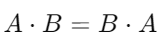
Propiedad Distributiva

Si tenemos más de un vector, podemos distribuir el producto escalar sobre una suma de vectores. Esto facilita mucho el cálculo cuando trabajamos con combinaciones de varios vectores.

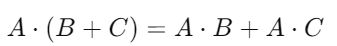
Propiedad Escalar

Si multiplicamos un vector A por un número escalar k, el producto escalar con otro vector B se ve afectado por ese número k de una forma proporcional.

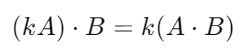
Fórmula del producto escalar

La fórmula general para calcular el producto escalar entre dos vectores A y B es:

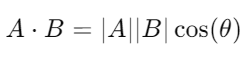
Donde:

• |A| y |B| son los módulos (o longitudes) de los vectores.
• θ es el ángulo entre los dos vectores.
• cos(θ) es el coseno del ángulo.

Este producto nos permite conocer la relación entre los vectores y obtener información sobre su orientación.

Cálculo del producto escalar

Para calcular el producto entre dos vectores, solo necesitamos conocer sus componentes. Imaginemos los vectores A y B en un espacio tridimensional, como por ejemplo:

A=(a₁,a₂,a₃) y B=(b₁,b₂,b₃)

El producto escalar se calcularía multiplicando cada componente correspondiente y sumando sus resultados:

A⋅B=a₁b₁+a₂b₂+a₃b₃

Ejemplo: Si A=(2,3,1) y B=(1,−1,4), el producto escalar sería:

A⋅B=(2)(1)+(3)(−1)+(1)(4)=2−3+4=3

Por tanto, el resultado del producto escalar entre estos dos vectores es 3.

Cálculo del módulo de un vector utilizando el producto escalar

El módulo o longitud de un vector es la medida de su tamaño. Esto significa que si realizas el producto escalar de un vector consigo mismo, obtienes el cuadrado de su módulo:

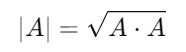
Ejemplo: Para el vector A=(3,4), su módulo sería:

A⋅A=3²+4²=9+16=25

Entonces, el módulo es:

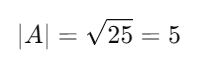
Este método es útil cuando solo tienes los componentes del vector y quieres saber su longitud.

Cálculo del ángulo entre dos vectores utilizando el producto escalar

Este producto también es útil para calcular el ángulo entre dos vectores. A partir de la fórmula original del producto escalar, podemos despejar el ángulo θ:

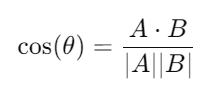
Ejemplo: Si A=(1,2) y B=(3,4), primero calculamos el producto escalar y los módulos:

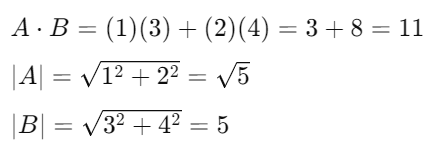
El coseno del ángulo es:

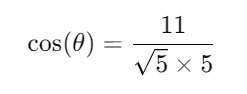
Calculando el valor final:

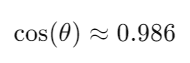
Por lo tanto, el ángulo θ es muy pequeño, lo que significa que los vectores están casi alineados.

Interpretación geométrica del producto escalar

El producto escalar además de servir para hacer cálculos, tiene una interpretación geométrica muy importante. Cuando hablamos de vectores, podemos imaginar líneas que tienen una magnitud (o longitud) y una dirección en el espacio. Por lo que, mide cómo de «alineados» están dos vectores o en otras palabras, cuánta influencia tiene uno sobre el otro en términos de dirección.

La proyección de un vector sobre otro

Imagina que tenemos dos vectores, A y B, en un espacio bidimensional o tridimensional. La proyección del vector A sobre otro vector B es en definitiva, cuánto del vector A está apuntando en la dirección de B.

Si los dos vectores están completamente alineados (en la misma dirección), el producto escalar será máximo. Mientras que si son perpendiculares, será cero porque A no tiene ninguna componente en la dirección de B.

Esto lo podemos visualizar pensando en una linterna proyectando una sombra. Si un vector es como una linterna y el otro como una superficie, el producto escalar nos dice cuánta «sombra» proyecta un vector sobre el otro.

¿Qué pasa si los vectores son perpendiculares?

Cuando el ángulo entre dos vectores es de 90 grados, es decir, cuando son perpendiculares, el producto escalar es cero. Esto tiene sentido geométricamente porque cuando dos vectores están perpendiculares entre sí, no hay ninguna componente de un vector que «apunte» en la dirección del otro.

Por ejemplo, si tenemos un vector A que apunta hacia el este y otro vector B que apunta hacia el norte, no hay una forma en la que uno de los vectores influya en la dirección del otro. Por eso, el producto escalar entre estos dos vectores es cero.

¿Qué pasa si los vectores son paralelos o casi paralelos?

Si los dos vectores apuntan exactamente en la misma dirección, el producto escalar es igual al producto de las magnitudes de los vectores. En este caso, θ es igual a 0 grados, y como el coseno de 0 grados es 1, la fórmula sería:

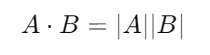
Esto significa que el producto escalar será el valor máximo posible para esos vectores, ya que están perfectamente alineados.

En el caso de que los vectores sean antiparalelos (apuntan en direcciones opuestas), el ángulo entre ellos será de 180 grados, y el coseno de 180 grados es -1. Por lo tanto, el producto escalar será negativo, lo que indica que los vectores están en direcciones completamente opuestas.

Ejemplo gráfico de proyección de un vector sobre otro

Para visualizar mejor, pensemos en dos vectores A y B en el plano. Supón que A es un vector largo que apunta hacia la derecha y B es un vector más corto que forma un ángulo agudo con A. El producto escalar nos permite encontrar la proyección de B sobre A.

1. Si el ángulo entre A y B es pequeño (es decir, están casi en la misma dirección), la proyección será grande y el producto escalar tendrá un valor alto.
2. Si el ángulo es de 90 grados (vectores perpendiculares), la proyección será cero, y el producto escalar también será cero.
3. Si el ángulo es mayor a 90 grados pero menor a 180 grados, la proyección será negativa, lo que significa que B está en una dirección opuesta a A, y por tanto, el producto escalar será negativo.

Por tanto, en resumen podemos decir que:

• Producto escalar positivo: los vectores están en la misma dirección o en direcciones cercanas.
• Producto escalar cero: los vectores son perpendiculares, no tienen componentes comunes en ninguna dirección.
• Producto escalar negativo: los vectores están en direcciones opuestas o casi opuestas.