Propiedades logaritmos: ¿Cuáles son?

Un logaritmo se define como el exponente al que un número específico, conocido como base, debe ser elevado para obtener otro número. Partiendo de su definición vamos a profundizar en todas las propiedades de los logaritmos.

Su importancia radica en su capacidad para transformar operaciones multiplicativas complejas en sumas más manejables, facilitando así el cálculo con números grandes y la resolución de ecuaciones exponenciales. En este artículo, exploraremos las propiedades fundamentales de los logaritmos, proporcionando una comprensión clara y detallada de su funcionamiento y aplicaciones.

¿Cuales son las propiedades de los logaritmos?

Las principales propiedades de los logaritmos se derivan de su definición y son esenciales para trabajar eficientemente con logaritmos en diversos campos de las matemáticas. Las propiedades principales incluyen:

1. Propiedad del Producto: El logaritmo de un producto es igual a la suma de los logaritmos de los factores individuales.
   • log_b​(m⋅n)=log_b​(m)+log_b​(n)
2. Propiedad del Cociente: El logaritmo de un cociente es igual al logaritmo del numerador menos el logaritmo del denominador.
   • log_b​(n/m​)=log_b​(m)−log_b​(n)
3. Propiedad de la Potencia: El logaritmo de una potencia es igual al exponente multiplicado por el logaritmo de la base de la potencia.
   • log_b​(mⁿ)=n⋅log_b​(m)
4. Propiedad del Cambio de Base: Permite convertir un logaritmo de una base a otra. Si tienes un logaritmo en base b y quieres convertirlo a base k, puedes usar la fórmula:
   • log_b​(a)=[log_k​(b)]/[log_k​(a)​]
5. Propiedad del Logaritmo de 1: El logaritmo de 1 en cualquier base es 0, ya que cualquier número elevado a la potencia de 0 es 1.
   • log_b​(1)=0
6. Propiedad del Logaritmo de la Base: El logaritmo de la base en sí mismo es siempre 1, ya que cualquier número elevado a la potencia de 1 es él mismo.
   • log_b​(b)=1

Propiedades de los logaritmos neperianos

Los logaritmos neperianos, también conocidos como logaritmos naturales, se basan en la constante e (aproximadamente igual a 2.71828), y se denotan como ln(x). A pesar de la base específica, los logaritmos neperianos comparten muchas de las propiedades generales de los logaritmos, adaptadas a la base e. Aquí están las propiedades principales de los logaritmos neperianos:

1. Propiedad del Producto: El logaritmo natural de un producto es igual a la suma de los logaritmos neperianos de los factores individuales.
   • ln(m⋅n)=ln(m)+ln(n)
2. Propiedad del Cociente: El logaritmo natural de un cociente es igual al logaritmo natural del numerador menos el logaritmo neperiano del denominador.
   • ln(n/m​)=ln(m)−ln(n)
3. Propiedad de la Potencia: El logaritmo natural de una potencia es igual al exponente multiplicado por el logaritmo natural de la base de la potencia.
   • ln(mⁿ)=n⋅ln(m)
4. Propiedad del Logaritmo de 1: El logaritmo natural de 1 es 0, ya que cualquier número elevado a la potencia de 0 es 1.
   • ln(1)=0
5. Propiedad del Logaritmo de e: El logaritmo neperiano de e es siempre 1, ya que e elevado a la potencia de 1 es e.
   • ln(e)=1
6. Propiedad de la Función Exponencial: La función exponencial y el logaritmo natural son funciones inversas.
   • e^ln(x)=x y ln(e^x)=x1

Propiedades de los logaritmos al simplificar logaritmos compuestos

Las propiedades de los logaritmos no solo facilitan la simplificación de expresiones logarítmicas sino que también permiten la manipulación de estas expresiones para resolver ecuaciones y problemas complejos.

1. El logaritmo de un producto de números es igual a la suma de los logaritmos individuales. Facilita la simplificación de logaritmos de números grandes en la suma de logaritmos más manejables.
2. El logaritmo de un cociente de números es igual al logaritmo del numerador menos el logaritmo del denominador. Útil para simplificar expresiones logarítmicas con divisiones.
3. En expresiones más complejas que involucran una combinación de productos, cocientes y potencias, se pueden aplicar estas propiedades en secuencia para simplificar la expresión paso a paso.

Regla del cambio de base en logaritmos

La regla del cambio de base en logaritmos es una herramienta útil para convertir logaritmos de una base a otra, facilitando cálculos y comparaciones.

Se utiliza cuando la base original dificulta el cálculo, permitiendo trabajar con bases más manejables. A continuación, se detallan las situaciones en las que se utiliza la regla del cambio de base y su utilidad:

1. Cálculo de Logaritmos en Bases No Estándar: En muchas situaciones, especialmente en cálculos manuales o en ciertas calculadoras, calcular logaritmos en bases que no son 10 o e (base del logaritmo natural) puede ser complicado o directamente imposible. La regla del cambio de base permite convertir estos logaritmos a una base más manejable, como 10 o e, facilitando así su cálculo.
2. Comparación de Logaritmos con Diferentes Bases: Al comparar logaritmos con diferentes bases, directamente no es posible hacer una comparación efectiva. La regla del cambio de base permite convertir todos los logaritmos a una base común, haciendo posible una comparación directa.
3. Simplificación de Expresiones Logarítmicas en Problemas Complejos: En problemas algebraicos o de cálculo que involucran logaritmos con bases diferentes, convertir todos los logaritmos a una base común puede simplificar significativamente la resolución del problema.

La regla del cambio de base en logaritmos se expresa matemáticamente de la siguiente manera:

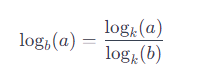
donde log_b​(a) es el logaritmo de a en la base b, y k es la nueva base a la que se quiere convertir el logaritmo. Comúnmente, k se elige como 10 o e debido a su presencia en calculadoras y su relevancia en muchas aplicaciones matemáticas.

¿Qué propiedades de los logaritmos se aplican al resolver inecuaciones logarítmicas?

Las inecuaciones logarítmicas son desigualdades que incluyen logaritmos y su resolución es fundamental en diversos campos de la matemática y la ingeniería. Resolver estas inecuaciones implica entender cómo las propiedades de los logaritmos interactúan con las reglas de las desigualdades. A continuación, se detallan las propiedades y técnicas clave utilizadas en la resolución de inecuaciones logarítmicas:

1. Propiedad de la Monotonía de los Logaritmos: Los logaritmos son funciones monótonas, lo que significa que si la base del logaritmo es mayor que 1 (b>1), la función logarítmica es creciente. Por el contrario, si 0<b<1, la función es decreciente. Esta propiedad es crucial al resolver inecuaciones, ya que el sentido de la desigualdad cambiará dependiendo de si la base del logaritmo es mayor o menor que 1.
2. Uso de la Definición de Logaritmo: Convertir la inecuación logarítmica a su forma exponencial equivalente a menudo simplifica el problema, permitiendo una resolución más directa. Recordemos que si log_b​(x)=y, entonces b^y=x.
3. Aplicación de Propiedades de Logaritmos en la Simplificación: Las propiedades de los logaritmos, como la propiedad del producto, del cociente y de la potencia, pueden ser utilizadas para simplificar las inecuaciones logarítmicas antes de resolverlas.
4. Cambio de Base para Comparación: Al igual que en ecuaciones logarítmicas, la regla del cambio de base puede ser utilizada para convertir logaritmos de diferentes bases a una base común, facilitando la comparación y resolución de la inecuación.
5. Consideraciones sobre el Dominio: Al resolver inecuaciones logarítmicas, es crucial recordar que el argumento del logaritmo (el número dentro del logaritmo) debe ser siempre positivo.

¿Cuál es la propiedad que establece la relación entre logaritmos y potencias de 1?

La propiedad establece que el logaritmo de 1 en cualquier base es igual a 0. Matemáticamente, se expresa como:

log_b​(1)=0 para cualquier base b>0, b=1

Esta propiedad se deriva directamente de la definición de logaritmo. Recordemos que el logaritmo log_b​(a) es el exponente al que se debe elevar la base b para obtener a. Si aplicamos esta definición con a=1, nos damos cuenta de que cualquier número (excepto 0) elevado a la potencia de 0 es igual a 1. Por lo tanto, independientemente de la base, el logaritmo de 1 siempre será 0.