Teorema de Bayes: Definición, formula y ejemplos

El Teorema de Bayes, nombrado así en honor al matemático inglés Thomas Bayes, es un pilar fundamental en el campo de la estadística y la probabilidad. Este teorema se formuló en el siglo XVIII, aunque su publicación fue postuma, gracias a la labor de otro matemático, Richard Price.

La importancia de este teorema radica en su capacidad para calcular probabilidades condicionales, es decir, la probabilidad de un evento dado el conocimiento de otros eventos relacionados.

La capacidad de revisar robabilidades a medida que se dispone de nueva información es crucial en un mundo donde los datos son abundantes y continuamente actualizados.

¿Qué es el Teorema de Bayes?

El Teorema de Bayes es una fórmula matemática utilizada para calcular la probabilidad de un evento basándose en el conocimiento previo de condiciones que podrían estar relacionadas con el evento.

En su esencia, este teorema trata sobre la actualización de nuestras probabilidades a medida que obtenemos nueva información. Es un enfoque para entender cómo el conocimiento previo (denominado probabilidad previa) se combina con nueva evidencia para formar una probabilidad actualizada (probabilidad posterior).

Dentro de la teoría de la probabilidad, el Teorema de Bayes ofrece un marco para pensar acerca de la probabilidad de eventos en términos de conocimientos o creencias previos y su actualización con nueva evidencia. Este enfoque contrasta con la interpretación normal de la probabilidad, que considera la probabilidad de un evento en términos de la frecuencia con la que ocurre en una serie de ensayos repetidos.

Fórmula del Teorema de Bayes

La fórmula del Teorema de Bayes es una ecuación matemática que expresa cómo una probabilidad condicional puede ser recalculada y actualizada con nueva evidencia. La fórmula es la siguiente:

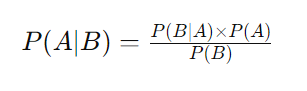
Donde:

• P(A∣B) es la probabilidad posterior de A dado B, es decir, la probabilidad de A después de tener en cuenta B.
• Es el resultado del cálculo y representa la probabilidad actualizada de A después de tener en cuenta la nueva evidencia B. Este es el foco principal del Teorema de Bayes, mostrando cómo la creencia inicial se modifica en la luz de los nuevos datos.
• P(B∣A) es la probabilidad de B dado que A es cierto. Esta es la probabilidad de observar el evento B dado que el evento A ha ocurrido. Esta parte de la fórmula incorpora la nueva evidencia que se está considerando.
• P(A) es la probabilidad previa de A, antes de considerar la evidencia B. Es la probabilidad de que el evento A ocurra antes de considerar la nueva evidencia. Representa el conocimiento o la creencia previa sobre A.
• P(B) es la probabilidad total de B, que actúa como un factor normalizador. Actúa como un factor de normalización para asegurar que las probabilidades sumen uno. Esta probabilidad considera todas las formas posibles en las que B podría ocurrir.

Esta fórmula permite calcular la probabilidad de un evento A dada la ocurrencia de otro evento B, utilizando el conocimiento previo de las probabilidades involucradas.

Aplicaciones Prácticas del Teorema de Bayes

En el campo de la ciencia de datos, el Teorema de Bayes tiene una amplia gama de aplicaciones, desde el análisis predictivo hasta el aprendizaje automático. Por ejemplo, se utiliza en algoritmos de clasificación bayesiana, que son fundamentales en el filtrado de spam en correos electrónicos. Estos algoritmos calculan la probabilidad de que un mensaje sea spam basándose en la frecuencia de ciertas palabras, actualizando sus estimaciones a medida que reciben nuevos datos.

En el sector financiero, el Teorema de Bayes se emplea para evaluar riesgos y tomar decisiones de inversión informadas. Las empresas pueden usarlo para predecir tendencias del mercado o para evaluar la probabilidad de éxito de un nuevo producto, basándose en datos históricos y tendencias actuales.

En medicina, se aplica para interpretar resultados de pruebas diagnósticas, ayudando a los médicos a tomar decisiones más informadas sobre tratamientos y diagnósticos. Al considerar la prevalencia de una enfermedad y la precisión de una prueba, los médicos pueden usar el Teorema de Bayes para estimar la probabilidad de que un paciente tenga una condición específica.

Ejemplos del Teorema de Bayes

Para ilustrar cómo se utiliza el Teorema de Bayes en la práctica, consideremos un ejemplo sencillo pero ilustrativo. Imagina que una prueba médica para una enfermedad particular tiene una precisión del 95% (es decir, la probabilidad de obtener un resultado verdadero positivo es del 95%, y la probabilidad de obtener un verdadero negativo es también del 95%). Si la enfermedad está presente en el 1% de la población, ¿cuál es la probabilidad de que una persona tenga realmente la enfermedad si obtiene un resultado positivo en la prueba?

1. Definición de las Probabilidades:
   • Probabilidad previa de tener la enfermedad P(Enfermedad)): 0.01 (1%)
   • Probabilidad de un resultado positivo dado que la persona tiene la enfermedad P(Positivo∣Enfermedad)): 0.95 (95%)
   • Probabilidad de un resultado positivo dado que la persona no tiene la enfermedad P(Positivo∣NoEnfermedad)): 0.05 (5%, ya que la prueba tiene un 95% de precisión)
2. Aplicación del Teorema de Bayes:
   • Utilizamos la fórmula: P(Enfermedad∣Positivo)=P(Positivo)P(Positivo∣Enfermedad)×P(Enfermedad)​
   • La probabilidad total de un resultado positivo, P(Positivo), se calcula teniendo en cuenta ambos casos (tener y no tener la enfermedad).
3. Cálculo de la Probabilidad Total de un Resultado Positivo:
   • P(Positivo)=P(Positivo∣Enfermedad)×P(Enfermedad)+P(Positivo∣NoEnfermedad)×P(NoEnfermedad)
   • P(Positivo)=0.95×0.01+0.05×0.99
4. Cálculo Final de la Probabilidad Posterior:
   • Sustituyendo estos valores en la fórmula original, obtenemos la probabilidad posterior.
5. La interpretación de los resultados del Teorema de Bayes depende del contexto y del significado de las probabilidades involucradas. En nuestro ejemplo, el resultado nos da la probabilidad de que alguien realmente tenga la enfermedad dada una prueba positiva, teniendo en cuenta la precisión de la prueba y la prevalencia de la enfermedad en la población general.

Resumen del Teorema de Bayes

• El Teorema de Bayes calcula la probabilidad de un evento basándose en conocimientos previos y nueva evidencia.
• Considera las probabilidades como grados de creencia que se actualizan con información adicional.
• Ampliamente usado en ciencia de datos, medicina y finanzas para análisis predictivos y decisiones informadas.
• Fundamental en estadística para la inferencia y toma de decisiones en situaciones inciertas.