Volumen de una Esfera: Fórmula y Aplicaciones

En este artículo, exploraremos en profundidad el concepto del volumen de una esfera. Comenzaremos con la fórmula básica para su cálculo, seguida de una discusión sobre la relación entre el radio de la esfera y su volumen. También abordaremos las unidades de medida típicas utilizadas para expresar el volumen, cómo los cambios en el radio afectan el volumen de la esfera, y la diferencia entre el área de la superficie y el volumen de una esfera.

Para ello en primer lugar vamos a hacer una breve introdución de los dos conceptos principales independientemente:

• El volumen nos permite cuantificar el espacio ocupado por un objeto tridimensional, ofreciendo una medida concreta de su capacidad o extensión.
• Una esfera es una figura geométrica perfectamente redonda en tres dimensiones, donde todos los puntos de la superficie están a la misma distancia del centro.

Volumen de una esfera formula

El volumen de una esfera es la cantidad de espacio que ocupa en tres dimensiones.

Para responder a la pregunta de cómo calcular el volumen de una esfera necesitamos conocer la fórmula del volumen de una esfera:

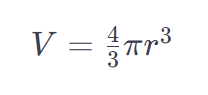
Donde:

• V representa el volumen de la esfera.
• r es el radio de la esfera, que es la distancia desde el centro de la esfera hasta cualquier punto en su superficie.
• π (pi) es una constante matemática cuyo valor aproximado es 3.14159, aunque generalmente se puede utilizar una versión redondeada como 3.14.

Esta fórmula simple demuestra la relación directa entre el radio y el volumen. La presencia de π (pi) refleja la conexión intrínseca de la esfera con el círculo.

Unidad de medida del volumen de una esfera

Las unidades de medida proporcionan una forma estandarizada de comunicar la magnitud del volumen, permitiendo comparaciones y cálculos precisos.

La unidad de medida del volumen de una esfera segun el Sistema Internacional de Unidades (SI) es el Metro cúbico (m³).

Es importante tener la capacidad de convertir entre estas unidades, especialmente en contextos internacionales o multidisciplinarios. Las conversiones permiten que los cálculos y las comparaciones sean coherentes y precisos, independientemente del sistema de unidades utilizado.

Ejemplo de cómo calcular el volumen de una esfera

Datos: Radio de la esfera (r): 3 cm

Cálculo:

1. Sustituye el valor del radio en la fórmula: V=3/4​π(3cm)³
2. Calcula el cubo del radio: (3cm)³=27cm³
3. Multiplica por π y 4/3​:
   • V=3/4​π×27cm³
   • V≈34​×3.14159×27cm³
   • V≈113.097cm³

Resultado: El volumen de la esfera es aproximadamente 113.097 cm³.

Relación cúbica del radio con el volumen de una esfera

El radio de una esfera es determinante de su volumen total, estableciendo una relación no lineal, sino cúbica, lo que significa que pequeños cambios en el radio pueden tener un gran impacto en el volumen total.

Esto significa que si duplicamos el radio de una esfera (multiplicamos por 2), el volumen no se duplica, sino que se multiplica por 2³=8

Implicaciones:

1. Sensibilidad al Cambio: Pequeños cambios en el radio resultan en grandes cambios en el volumen, crucial en el diseño y comprensión de fenómenos naturales.
2. Eficiencia de Espacio: La relación cúbica destaca la eficiencia de las esferas al maximizar el volumen con la menor superficie posible, común en formas naturales como células y planetas.
3. Cálculos de Escala: Comprender cómo el cambio en el radio afecta el volumen es esencial en modelización y diseño, permitiendo escalas precisas en ingeniería y fabricación.

Diferencia entre área de superficie y volumen de una esfera

Para conocer la diferencia entre el area y el volumen de una esfera en primer lugar vamos a comparar ambos conceptos.

Área:

• Es una medida bidimensional que se refiere a la cantidad total de espacio que cubre la superficie exterior de la esfera. Se calcula usando la fórmula
• Fórmula: A = 4πr²
• Se expresa en unidades cuadradas (metros cuadrados, centímetros cuadrados, etc.).

Volumen:

• El volumen de una esfera, por otro lado, mide la cantidad total de espacio tridimensional que ocupa la esfera.
• Fórmula: V=(4/3)πr³
• Unidades cúbicas (metros cúbicos, centímetros cúbicos).

Diferencias clave:

1. Dimensionalidad: Área de superficie es bidimensional, volumen es tridimensional.
2. Unidades: Área de superficie se mide en unidades cuadradas, volumen en unidades cúbicas.
3. Relación con el Radio: Área proporcional a ( r^2 ), volumen proporcional a ( r^3 ). El volumen aumenta más rápidamente con el aumento del radio.

¿Existen fórmulas alternativas para calcular el volumen de una esfera?

Aunque para calcular el volumen de una esfera la forma mas simple y utilizada es la que hemos comentado anteriormente, en ciertos contextos, pueden utilizarse enfoques alternativos. Aqui te exponemos brevemente algunos:

• La Integración en Coordenadas Cartesianas emplea cálculo integral en tres dimensiones, integrando la función de una semiesfera y multiplicando por dos. Común en campos como la física e ingeniería.
• El Método de Discos o Anillos (Cálculo) es una técnica de integración que deriva la fórmula de volumen de una esfera al aplicarla a la circunferencia de un círculo. Se utiliza para calcular el volumen de sólidos de revolución
• El Principio de Cavalieri establece que sólidos con igual altura y secciones transversales tienen igual volumen, permitiendo comparar una esfera con un sólido de forma conocida. La Relación con el Volumen de Otros Sólidos establece conexiones entre el volumen de una esfera y otros sólidos geométricos como cilindros o conos mediante proporciones o relaciones específicas.

Puntos clave del volumen de una esfera

1. Fórmula: El volumen de una esfera se calcula mediante la fórmula (4/3) * π * r^3, donde «r» es el radio de la esfera.
2. Unidad de medida: Metro cúbico (m³).
3. Valor de π: π (pi) es una constante matemática aproximada a 3.14159 que se utiliza en la fórmula.
4. Significado: El volumen de una esfera representa la cantidad de espacio tridimensional que ocupa y se aplica en matemáticas, física, ingeniería y otras disciplinas científicas.